Last September, I gave a talk which included a bunch of two-dimensional plots of a high-dimensional objective I was developing specialized algorithms for optimizing. A month later, at least three of my colleagues told me that my plots had inspired them to make similar plots. The plotting trick is really simple and not original, but nonetheless I'll still write it up for all to enjoy.

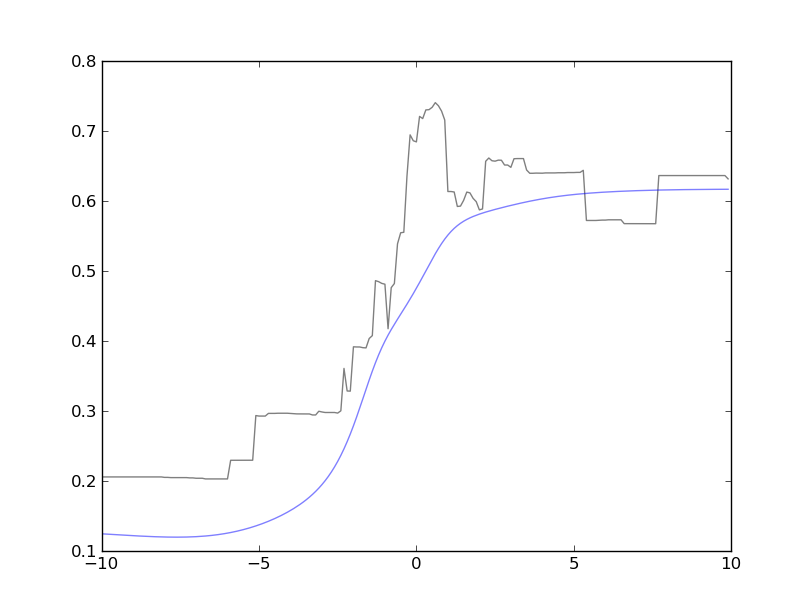
Example plot: This image shows cross-sections of two related functions: a non-smooth (black) and a smooth approximating function (blue). The plot shows that the approximation is faithful to the overall shape, but sometimes over-smooths. In this case, we miss the maximum, which happens near the middle of the figure.

Details: Let \(f: \mathbb{R}^d \rightarrow \mathbb{R}\) be a high-dimensional function (\(d \gg 2\)), which you'd like to visualize. Unfortunately, you are like me and can't see in high-dimensions what do you do?

One simple thing to do is take a nonzero vector \(\boldsymbol{d} \in \mathbb{R}^d\), take a point of interest \(\boldsymbol{x}\), and build a local picture of \(f\) by evaluating it at various intervals along the chosen direction as follows,

Of course, you'll have to pick a reasonable range and discretize it. Note, \(\boldsymbol{x}\) and \(\boldsymbol{d}\) are fixed for all \(\alpha_i\). Now, you can plot \((\alpha_i,f_i)\).

Picking directions: There are many alternatives for picking \(\boldsymbol{d}\), my favorites are:

1. Coordinate vectors: Varying one (or two) dimensions.

2. Gradient (if it exists), this direction is guaranteed to show a local increase/decrease in the objective, unless it's zero because we're at a local optimum. Some variations on "descent" directions:

   • Use the gradient direction of a different objective, e.g., plot (nondifferentiable) accuracy on dev data along the (differentiable) likelihood direction on training data.

   • Optimizer trajectory: Use PCA on the optimizer's trajectory to find the directions which summarize the most variation.

3. The difference of two interesting points, e.g., the start and end points of your optimization, two different solutions.

4. Random:

   If all your parameters are on an equal scale, I recommend directions drawn from a spherical Gaussian.¹ The reason being that such a vector is uniformly distributed across all unit-length directions (i.e., the angle of the vector, not it's length). We will vary the length ourselves via \(\alpha\).

   However, often components of \(\boldsymbol{x}\) have different scales, so finding a "natural scale" is crucial if we are going to draw conclusions that require a comparison of the perturbation sensitivities across several dimensions—this is closely related to why we like second-order and adaptive optimization algorithms (discussion); \(\boldsymbol{d}\)'s units must match the units of \(\boldsymbol{x}\) in each coordinate!

5. Maximize "interestingness": You can also use a direction-optimization procedure to maximize some measure of "interestingness" (e.g., the direction in which training and dev loss differ the most; the "bumpiest" direction or direction taking the biggest range of values).

Extension to 3d: It's pretty easy to extend these ideas to generating three-dimensional plots by using two vectors, \(\boldsymbol{d_1}\) and \(\boldsymbol{d_2},\) and varying two parameters \(\alpha\) and \(\beta\),

Closing remarks: These types of plots are probably best used to: empirically verify/explore properties of an objective function, compare approximations, test sensitivity to certain parameters/hyperparameters, visually debug optimization algorithms.

Further reading:

• Visualizing the Loss Landscape of Neural Nets

Footnotes

1. More formally, vectors drawn from a spherical Gaussian are points uniformly distributed on the surface of a \(d\)-dimensional unit sphere, \(\mathbb{S}^d\). Sampling a vector from a spherical Gaussian is straightforward: sample \(\boldsymbol{d'} \sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\), \(\boldsymbol{d} = \boldsymbol{d'} / \| \boldsymbol{d'} \|_2\) ↩